Il modulo di Poisson (indicato anche come coefficiente di Poisson, coefficiente di contrazione trasversale o rapporto di Poisson) è una caratteristica propria di ciascun materiale (dipendente dalla temperatura) che misura, in presenza di una sollecitazione monodirezionale longitudinale, il grado in cui il campione di materiale si restringe o si dilata trasversalmente.
È definito come:
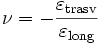
dove ν è il modulo di Poisson, 
è la deformazione trasversale, 
è la deformazione longitudinale.
Il modulo di Poisson è un coefficiente adimensionale, con l'attenzione di osservare che tale relazione vale solo in uno stato di sollecitazione monodirezionale. In stati tensionali più complessi tale relazione non è più verificata ed il modulo di Poisson non coincide più con tale rapporto.
Il modulo di Poisson è correlato al modulo di elasticità ed al modulo di taglio dalla seguente relazione:
è la deformazione trasversale, è la deformazione longitudinale.Il modulo di Poisson è un coefficiente adimensionale, con l'attenzione di osservare che tale relazione vale solo in uno stato di sollecitazione monodirezionale. In stati tensionali più complessi tale relazione non è più verificata ed il modulo di Poisson non coincide più con tale rapporto.
Il modulo di Poisson è correlato al modulo di elasticità ed al modulo di taglio dalla seguente relazione:
Valori limite per il modulo di Poisson ν
I valori del modulo di Poisson per materiali reperibili in natura sono compresi tra 0 e 0,5; il valore massimo corrisponde ad un materiale virtualmente incomprimibile (la gomma, ad esempio, ha valori prossimi a 0,5), mentre il valore minimo corrisponde ad un materiale con modulo di taglio tendente ad infinito.
Esiste tuttavia una famiglia di materiali, chiamati auxetici (per esempio il Gore-Tex), per i quali il modulo di Poisson può essere negativo: questo comporta, a seguito di una prova di trazione monoassiale, la presenza di deformazioni estensionali normali all'asse di sollecitazione di carattere positivo (ovvero un'estensione del materiale in direzione ortogonale a quella di sollecitazione), visto il legame che intercorre tra sforzi normali applicati e deformazioni normali conseguenti dettato dalla legge di Hooke (espressa in forma tensoriale) per materiali omogenei e isotropi.
Il campo di valori che compete al coefficiente di Poisson ν, dunque, risulta essere variabile tra −1 e 0,5:
I valori del modulo di Poisson per materiali reperibili in natura sono compresi tra 0 e 0,5; il valore massimo corrisponde ad un materiale virtualmente incomprimibile (la gomma, ad esempio, ha valori prossimi a 0,5), mentre il valore minimo corrisponde ad un materiale con modulo di taglio tendente ad infinito.
Esiste tuttavia una famiglia di materiali, chiamati auxetici (per esempio il Gore-Tex), per i quali il modulo di Poisson può essere negativo: questo comporta, a seguito di una prova di trazione monoassiale, la presenza di deformazioni estensionali normali all'asse di sollecitazione di carattere positivo (ovvero un'estensione del materiale in direzione ortogonale a quella di sollecitazione), visto il legame che intercorre tra sforzi normali applicati e deformazioni normali conseguenti dettato dalla legge di Hooke (espressa in forma tensoriale) per materiali omogenei e isotropi.
Il campo di valori che compete al coefficiente di Poisson ν, dunque, risulta essere variabile tra −1 e 0,5:
| materiale | modulo di Poisson |
|---|---|
| gomma | ~ 0,50 |
| oro | 0,42 |
| argilla satura | 0,40-0,50 |
| magnesio | 0,35 |
| titanio | 0,34 |
| rame | 0,33 |
| lega d'alluminio | 0,33 |
| argilla | 0,30-0,45 |
| acciaio inossidabile | 0,30-0,31 |
| acciaio | 0,27-0,30 |
| ghisa | 0,21-0,26 |
| sabbia | 0,20-0,45 |
| cemento | 0,20 |
| vetro | 0,18-0,30 |
| schiuma | 0,10-0,40 |
| sughero | ~ 0,00 |
| materiali auxetici | < 0 |
